杰拉斯的博客
[ACM]简单动态规划——电路布线
编程算法
电路布线
【问题描述】
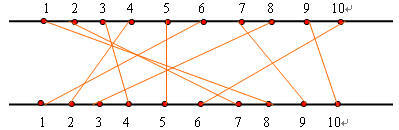
在一块电路板的上、下两端分别有n个接线柱。根据电路设计,要求用导线(i,π(i))将上端接线柱i与下端接线柱π(i)相连,如图所示。
其中,π(i),1<=i<=n是{1,2,…,n}的一个排列。导线(i,π(i))称为该电路板上的第i条连线。对于任何1<=i π(j)。
在制作电路板时,要求将这n条连线分布到若干绝缘层上。在同一层上的连线不相交。你的任务是要确定将哪些连线安排在第一层上,使得该层上有尽可能多的连线。换句话说,就是确定导线集Nets={ i,π(i),1<=i<=n}的最大不相交子集。
【输入形式】
输入文件第一行为整数n;第二行为用一个空格隔开的n个整数,表示π(i)。
【输出形式】
输出文件第一行为最多的连线数m,第2行到第m+1行输出这m条连线(i,π(i))。
[ACM]简单回溯——猜牌游戏
编程算法
猜牌游戏
【问题描述】
猜牌游戏:桌上有分别写着1-100的100张牌,游戏者从100张牌子中抽出K张,把K(1<K<100)张牌对应的数字相乘得到一个结果S,然后把结果S告诉挑战者,让挑战者猜游戏者K张牌的可能组合。游戏者也可能报一个假的结果S给挑战者,也就是不存在K张牌相乘得到该结果,这时挑战者要辨别游戏者是否说谎。挑战者猜中则为赢,猜错就为输。
【输入形式】
从标准输入自然数S和自然数K。
【输出形式】
输出K张牌的所有方式(用空格隔开),每一种方式为一行,在每一行末均输出一个回车符。如果不存在K张牌相乘得到S的情况,则输出LIE。
[ACM实验七]ACM程序设计基础(5)
编程算法
]实验项目:ACM程序设计基础(5)
实验目的:掌握C++程序设计基础。
实验要求:使用VC++6.0实现实验要求。
实验内容:
1.编写一个函数实现如下功能:
输入:7
输出:
1 8 14 19 23 26 28 2 9 15 20 24 27 3 10 16 21 25 4 11 17 22 5 12 18 6 13 7
输入:5
输出:
1 6 10 13 15
2 7 11 14
3 8 12
4 9
5
(提示:使用setw(int n)函数对齐,该函数在iomanip.h中,动态二维数组的程序如下:
int **a = new int*[n]; //n行 for(int i = 0; i < n; ++i) a[i] = new int[m]; //m列
2.由1..9这九个数字组成九位数(无重复数字)能被11整除,求最大、最小者。
3.附加题:
给定n个矩阵A1A2…An, 其中Ai与Ai+1是可乘的。考察这n个矩阵的连乘积A1A2..An,如何确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少。
例如A1=30×35、A2=35×15、A3=15×5、A4=5×10、A5=10×20、A6=20×25
最小乘数为15125。
[ACM_SMU_1104]最优矩阵连乘积
编程算法
最优矩阵连乘积
Accepted: 10 Total Submit: 18
Time Limit: 1000ms Memony Limit: 32768KB
Description
在科学计算中经常要计算矩阵的乘积。矩阵A和B可乘的条件是矩阵A的列数等于矩阵B的行数。若A是一个p×q的矩阵,B是一个q×r的矩阵,则其乘积C=AB是一个p×r的矩阵。其标准计算公式为:
由该公式知计算C=AB总共需要pqr次的数乘。
为了说明在计算矩阵连乘积时加括号方式对整个计算量的影响,我们来看一个计算3个矩阵{A1,A2,A3}的连乘积的例子。设这3个矩阵的维数分别为10×100,100×5和5×50。若按第一种加括号方式((A1A2)A3)来计算,总共需要10×100×5+10×5×50=7500次的数乘。若按第二种加括号方式(A1(A2A3))来计算,则需要的数乘次数为100×5×50+10×100×50=75000。第二种加括号方式的计算量是第一种加括号方式的计算量的10倍。由此可见,在计算矩阵连乘积时,加括号方式,即计算次序对计算量有很大影响。
于是,人们自然会提出矩阵连乘积的最优计算次序问题,即对于给定的相继n个矩阵{A1,A2,…,An}(其中Ai的维数为pi-1×pi ,i=1,2,…,n),如何确定计算矩阵连乘积A1A2…An的一个计算次序(完全加括号方式),使得依此次序计算矩阵连乘积需要的数乘次数最少。
Input
有若干种案例,每种两行,第一行是一个非负整数n表示矩阵的个数,n=0表示结束。接着有n行,每行两个正整数,表示矩阵的维数。
Ouput
对应输出最小的乘法次数。
[ACM实验六]ACM程序设计基础(4)
编程算法
实验项目:ACM程序设计基础(4)
实验目的:掌握C++程序设计基础。
实验要求:使用VC++6.0实现实验要求。
实验内容:
1.设有n个活动的集合E={1,2,…n},其中每个活动都要求使用同一资源,如演讲会场等,而在同一时间内只有一个活动能使用这一资源。每个活动i都有一个要求使用该资源的起始时间Si和一个结束时间Fi,且Si<Fi,求出最多可以安排多少个活动使用该资源,并给出一个安排方案,如:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Si | 12 | 5 | 0 | 3 | 8 | 5 | 2 | 8 | 3 | 6 | 1 |
| Fi | 14 | 7 | 6 | 5 | 12 | 9 | 13 | 11 | 8 | 10 | 4 |
最多安排的资源个数为4,安排方案为:11 2 8 1
Sample Input
11 12 14 5 7 0 6 3 5 8 12 5 9 2 13 8 11 3 8 6 10 1 4
Sample Output
11 2 8 1 (4)
2.用KMP算法实现实验,输入两个只包含小写字母的字符串,判断第二个字符串是否是第一个字符串的子串,是则输出第二字符串在第一个字符串的起始位置,不是则输出NO。例如:
输入:abedsadfdseg
dsa
输出:4
3. Crashing Balloon问题,见Crashing Balloon。