[ACM]简单动态规划——电路布线

杰拉斯 | 时间：2012-06-02, Sat | 21,050 views
编程算法　

电路布线

【问题描述】

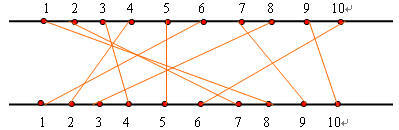
在一块电路板的上、下两端分别有n个接线柱。根据电路设计，要求用导线（i，π(i)）将上端接线柱i与下端接线柱π(i)相连，如图所示。

其中，π(i)，1<=i<=n是{1，2，…，n}的一个排列。导线（i，π(i)）称为该电路板上的第i条连线。对于任何1<=i π(j)。

在制作电路板时，要求将这n条连线分布到若干绝缘层上。在同一层上的连线不相交。你的任务是要确定将哪些连线安排在第一层上，使得该层上有尽可能多的连线。换句话说，就是确定导线集Nets={ i，π(i)，1<=i<=n}的最大不相交子集。

【输入形式】

输入文件第一行为整数n；第二行为用一个空格隔开的n个整数，表示π(i)。

【输出形式】

输出文件第一行为最多的连线数m，第2行到第m+1行输出这m条连线（i，π(i)）。

【输入样例】

【输出样例】

思路如下：

比较基础的动态规划问题，设a[i][j]为上端接线柱i与下端接线柱j前的最大不相交子集，则：

若i与j不相连，则i与j前的最大不想交子集等于i与j - 1前或i - 1与j前的最大不相交子集的最大值，即a[i][j] = max(a[i][j - 1], a[i - 1][j])
若i与j相连，则i与j前的最大不想交子集等于i - 1与j - 1前的最大不想交子集加1，即a[i][j] = a[i - 1][j - 1] + 1

#include<stdio.h>

inline int max(int a, int b){
	return a > b ? a : b;
}

int main(){
	int n, i, j;
	int a[100][100], b[100];
	a[0][0] = 0;
	scanf("%d", &n);
	for(i = 0; i < n; ++i){
		int j;
		scanf("%d", &j);
		scanf("%d", &b[j]);
		a[i][0] = 0;
		a[0][i] = 0;
	}
	for(i = 1; i <= n; ++i){
		for(j = 1; j <= n; ++j){
			if(b[i] == j){
				a[i][j] = a[i - 1][j - 1] + 1;
			}else{
				a[i][j] = max(a[i - 1][j], a[i][j - 1]);
			}
		}
	}
	printf("%d\n", a[n][n]);
	return 0;
}

如需转载请注明出处：杰拉斯的博客

杰拉斯的博客