[整理]ACM模拟题详解(3)——数论(续)
编程算法
5、Prime Ring Problem
Problem Description
A ring is compose of n circles as shown in diagram. Put natural number 1, 2, ..., n into each circle separately, and the sum of numbers in two adjacent circles should be a prime.
Note: the number of first circle should always be 1.
Input
n (0 < n < 20).
Output
The output format is shown as sample below. Each row represents a series of circle numbers in the ring beginning from 1 clockwisely and anticlockwisely. The order of numbers must satisfy the above requirements. Print solutions in lexicographical order.
You are to write a program that completes above process.
Print a blank line after each case.
Sample Input
6
8
Sample Output
Case 1:
1 4 3 2 5 6
1 6 5 2 3 4
Case 2:
1 2 3 8 5 6 7 4
1 2 5 8 3 4 7 6
1 4 7 6 5 8 3 2
1 6 7 4 3 8 5 2
翻译:n个数字(1,2,3...n)围成一个圈,要求相邻的两个数字之和是质数。题目要求根据给出的n,计算所有能够组成满足条件的圈的数字序列。
解题思路:
首先选择1,然后选择和1相加等于质数的数字,可能有很多种情况,例如(n=6的情况):
1+2
1+4
1+6
然后针对每种情况,再选择与第二个数的和为质数的数字,得到下面的序列
1+2+3
1+2+5
1+4+3
1+6+5
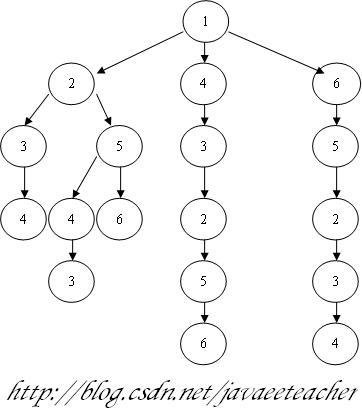
直到所有的数字都选择完,把所有的组合列出即可。计算的过程就是构造下面的树的过程。
从图中可以看出1-4-3-2-5-6 和 1-6-5-2-3-4是两个合法的解。
对于树的遍历可以采用深度优先,也可以采用广度优先,如果采用广度优先占用的内存比较大,所以解空间比较大的时候不宜采用。
下面是采用广度优先实现的(当n=18和n=20的时候内存不够用)
/*
* Prime Ring Problem
*/
public static void test4(int n){
int values[] = new int[n];
// 初始化
for(int i=0;i<n;i++){
values[i] = i+1;
}
// 表示遍历过程中可能的解
List list = new ArrayList();
list.add(values);
// 处理后面的n-1个数字,1永远是第一个
for(int i=1;i<n;i++){
List temp = list;
list = new ArrayList();
// 对于每个可能的解,得到下一层节点
for(int j=0;j<temp.size();j++){
int tempValues[]=(int[])temp.get(j);
// 考虑所有可能的组合
for(int k=i;k<n;k++){
if(isPrime(tempValues[i-1]+tempValues[k])){
// 创建新的状态,并复制原来的值
int[] newValues = Arrays.copyOf(tempValues, tempValues.length);
// 交换i和k处的值
if(i!=k){
int change = newValues[i];
newValues[i] = newValues[k];
newValues[k] = change;
}
// 把新状态添加到列表中
list.add(newValues);
}
}
}
}
// 输出结果
for(int i=0;i<list.size();i++){
int[] tempValues = (int[])list.get(i);
if(isPrime(tempValues[0]+tempValues[n-1])){
for(int j=0;j<n;j++){
System.out.print(tempValues[j]+" ");
}
System.out.println();
}
}
System.out.println(list.size());
}
下面是深度优先的算法。
/*
* Prime Ring Problem(深度优先)
*/
public static void test5(int n){
// 数组的前n个元素表示环中的数字,第n+1个数据表示数组中前n+1个元素是满足条件的
int values[] = new int[n+1];
// 初始化
for(int i=0;i<n;i++){
values[i] = i+1;
}
values[n]=1;
// 表示遍历过程中可能的解
List list = new ArrayList();
list.add(values);
StringBuffer sb = new StringBuffer();
while(list.size()>0){
// 取出第一个元素
int tempValues[]=(int[])list.get(0);
// 表示处理到第几层,第一层用0表示
int index=tempValues[n];
// 遍历并生成所有可能的下一层节点
for(int k=tempValues[n];k<n;k++){
if(isPrime(tempValues[index-1]+tempValues[k])){
// 如果是最后一层并且,最后一个数和第一个数的和
// 也是质数,则输出结果
if(index==n-1 && isPrime(tempValues[index]+1)){
for(int j=0;j<n;j++){
sb.append(tempValues[j]+" ");
}
sb.append("/n");
// 分批输出
if(sb.length()>10000){
System.out.print(sb.toString());
sb=new StringBuffer();
}
continue;
}
// 创建新的状态,并复制原来的值
int[] newValues = Arrays.copyOf(tempValues, tempValues.length);
// 交换i和k处的值
if(index!=k){
int change = newValues[index];
newValues[index] = newValues[k];
newValues[k] = change;
}
newValues[n] = newValues[n]+1;
// 把新状态添加到列表中,放在最前面,深度优先,
// 如果采用广度优先,则应该放到最后面
list.add(0,newValues);
}
}
// 从list中删除当前的节点
list.remove(tempValues);
}
System.out.print(sb.toString());
}
6、人见人爱A^B
Problem Description
求A^B的最后三位数表示的整数。
说明:A^B的含义是“A的B次方”
Input
输入数据包含多个测试实例,每个实例占一行,由两个正整数A和B组成(1<=A,B<=10000),如果A=0, B=0,则表示输入数据的结束,不做处理。
Output
对于每个测试实例,请输出A^B的最后三位表示的整数,每个输出占一行。
Sample Input
2 3
12 6
6789 10000
0 0
Sample Output
8
984
1
解题思路:要求6789的10000次方,使用Java语言提供的数据类型肯定要越界,可以使用之前介绍的大数解决方案,但是计算量会非常大。仔细看这道题会发现要求求结果的后3位,所以6789*6789与789*789的结果的后3位是相同的,所以在处理的时候只需要考虑后3位即可,这样处理解简单了。下面的代码供参考:
/*
* A的B次方的后3位
*/
public static int test6(int a,int b){
// 保留后3位
int temp = a%1000;
int result = temp;
for(int i=1;i<b;i++){
result = (result*temp)%1000;
}
return result;
}
如需转载请注明出处:杰拉斯的博客
当前暂无评论 »